- Title: Contemplations, A Logical Refutation of the Capitalistic Slogan.
- Author: Arvindus.
- Publisher: Arvindus.
- Copyright: Arvindus, 2010, all rights reserved.
- Index: 201006051.
- Edition: html, first edition.
Introduction
Before an action on a subject can be performed an idea of that subject must be formed. And the clearer the formed idea is, the more accurate the action may be performed. So when the action of a logical refutation is to be performed on the subject of the capitalistic slogan, first a clear idea of the latter must be formed. Thus we shall start this contemplation with a short exploration of the capitalistic slogan. After gaining clarity on this subject it may logically be refuted.
The Capitalistic Slogan
To clarify and explicate the capitalistic slogan first an idea should be formed of what capitalism is. Now much has been written and said about capitalism, both by proponents and opponents. In general both parties seem to agree on what capitalism is, but after that their ways part. Their further arguments then mostly consist of enumerating the pros or the cons of the system. With these we shall not deal much in this contemplation. What does spark our interest however is the answer to the question on which both parties have agreed upon to what capitalism is. Their mutual conclusions on this are reflected and concisely formulated in the English dictionary. According to the dictionary is capitalism a system which favours the existence of capitalists.1 And a capitalist in turn is in the dictionary considered to be someone who has accumulated capital or someone who has capital available for employment in financial or industrial enterprises.2 Thus capitalism is a system which favours the existence of persons who have accumulated capital which is available for employment in enterprises. Now this word 'employment' is ambiguous in this context. It makes that 'capital' may refer to capital which is available for investing in enterprises or to capital which is available for hiring laborers in enterprises. In this case the ambiguity does not matter much because here both readings are valid. Capitalism is a system which favours the existence of persons who have accumulated capital which is available for investing in, and hiring laborers for financial or industrial enterprises.
So then what is meant with 'the capitalistic slogan'? We have come to an idea of what capitalism is, and now an idea needs to be formed of what a slogan is. After having gained such an idea, both the ideas can be taken together again in their wholeness of the capitalistic slogan. So what is a slogan? The word comes from the Gaelic 'sluaghghairm', meaning 'war-cry'.3 Now a war is fought either for defense or for attack, and similarly are slogans linguistic expressions which are used to defend or to attack. What the capitalistic slogan aims to defend is of course capitalism and what it aims to attack is capitalism's enemies. Capitalism's war is linguistically also fought on more intellectual levels such as in long treatises. It is from those intellectual treatises that phrases are extracted to summarize the in the treatises presented ideas. Such phrases move from one person to another, presenting the ideas in a very summarized way. Eventually they become public slogans, recognized in their rootedness by some, but as such unrecognized by many. Now the capitalistic slogan meant in this contemplation is rooted in the idea that in the capitalistic system everybody has the opportunity to attain a high level of wellbeing.4 And this capitalistic idea is summarized in a phrase that has become the capitalistic slogan. This slogan and war-cry, used unthoughtfully by many pro-capitalists, goes approximately as follows: 'in capitalism everybody has the chance to be successful'.
Modal First Order Predicate Logic
For our logical refutation of the capitalistic slogan we shall make use of modal first order predicate logic. Logic structures arguments in order to decide upon their acceptability or their unacceptability.5 Modal first order predicate logic does this by explicating the subjects, predicates, quantifiers, conjunctions and modalities which may be present in an argument, and it explicates them by means of symbols. Subjects (in logic named 'singular terms') are symbolized by small letters (a, b, c, ..., in case of constants, …, x, y, z, in case of variables).6 The antique philosopher 'Socrates' for instance may be symbolized with 's'. Or the point in time '14 February 2010, 8.30 PM CET' for instance may be symbolized with 't1'. Predicates are symbolized by capital letters (A, B, C, …).7 And as predicates in sentences belong to subject, so are also the symbols logically written together. The assertion 'Immanuel Kant went for a walk on 14 February 1783 at 5.00 PM CET' for instance may be symbolized as 'Wkt1'. Quantifications are symbolized by the symbols '∀'and '∃'.8 If the universal quantifier '∀' is used in a logical formula it signifies that the assertion following this quantifier is valid for all existences that it binds. For instance a formula such as '∀xFx' may assert that all existences are finite. The existential quantifier '∃' is used to signify the existence of at least one existence. A formula such as '∃xHx' may assert that there is an existence which is a human. Connectives are symbolized by mathematical symbols such as '∧', '∨', '⇒', '⇔' and '¬'.9 These connectives connect subjects, predicated subjects and compound formulas. Of these connectives '∧' stands for '… and …', '∨' stands for '… or …', '⇒' stands for 'if … then …', '⇔' stands for '… is equivalent to …' and '¬' stands for 'it is not so that…'. For instance the formula '¬Fs⇒¬Hs' may assert that if it is not so that Socrates is finite then he is not a human. The well known equality symbol '=' is also used as a connective to indicate an identity. Other used mathematical symbols are brackets, which have a similar function in modal first order predicate logic as in mathematics. The logic operator which is placed just before the brackets is valid for the whole of the formula placed within the brackets. The formula '∃x(Fx∧x=s)' may assert that there is an existence which is finite and this existence is Socrates. As a conclusion to this very short introduction to modal first order predicate logic two modality symbols shall be given. These concern the symbols for 'necessity' and 'possibility', knowingly '□' and '◊'.10 The formula '□∀x(Hx⇒Fx)' may assert that it is necessary for all existences that if they are human then they are finite.
Basic Formulas
So let's now apply this modal first order predicate logic to the capitalistic slogan. This slogan was enunciated as: 'in capitalism everybody has a chance of being successful'. Before a logical formulation is possible first the domain and the translation keys should be set. As the domain we shall take all beings (a, b, c, …) and all points in time (t1, t2, t3, …). The translation keys we set as follows. 'C' stands for '…lives in a capitalistic system at time…'. 'S' stands for '…is successful at time…'. And 'H' stands for '…is human'.
Now with the domain and predicates defined we are able to formulate the capitalistic slogan as follows.
1) □∀x∀tα(Hx⇒(Cxtα⇒◊Sxtα))
This formula asserts that it is necessary for every being at every point in time that if this being is human then it is so that if he lives in a capitalistic system at a certain point in time then it is possible that he is successful at that point in time.
A deconstruction of this formula will show how it is structured and build up.
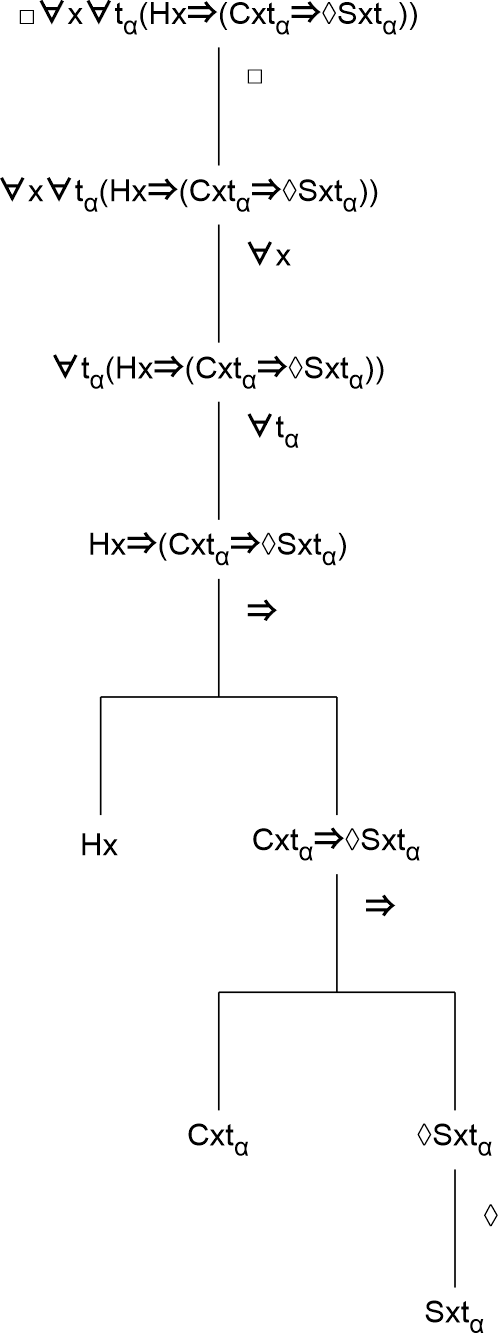
What this deconstruction among other things shows is that the sub formula 'Sxtα' is bound by the universal quantifiers '∀x' and '∀tα'. This means that if an actualization of the possibility of being successful takes places at a certain time (and this possibility is expressed by the sub formula '◊Sxtα'), then it will take place for all humans who live in a capitalistic system at that time (the last according to the sub formula 'Cxtα' which is also bound by '∀x' and '∀tα'). Thus this formula implies that if one human in a capitalistic system has the possibility for success then all such humans must have that possibility at the same time.11 All become successful or none become successful.
However the capitalistic slogan does not necessarily convey the logical assertion that all humans who are living in a capitalistic society have the possibility to be successful together at the same time. It may also assert that of all humans who are living in a capitalistic society only one or a few have the possibility to be successful at the same time and that that one or those few can be everybody. This is what the following formula asserts.
2) □∀x∀tα(Hx⇒(Cxtα⇒◊(∃y(Sytα∧x=y))))
This formula asserts that it is necessary for every being at every point in time that if this being is human then it is so that if he lives in a capitalistic system at a certain point in time then it is possible that there is a being who is successful at that point in time and that that being is the human who is placed in the capitalistic society. This formula can be deconstructed as follows.
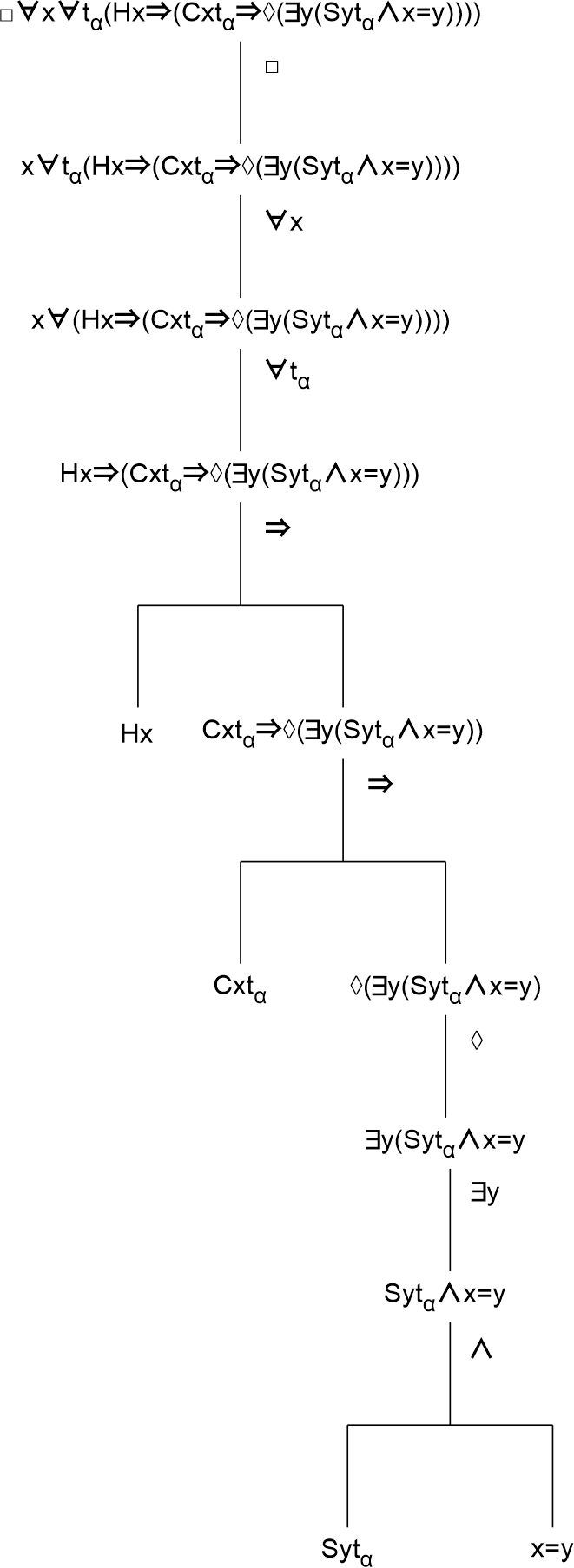
This deconstruction shows that the sub formula 'Sytα' is bound by the existential quantifier '∃y'. This already shows that an actualization of the possibility of being successful will not take place for all humans at the same time. But what may be actualized is the sub formula which is bound by the possible modality operator '◊', and this regards the sub formula '∃ySytα∧x=y'. Here '∃ySytα' expresses the individuality of the human or humans who may be successful. And 'x=y' expresses that this human or these humans belong to the ones living in a capitalistic system (because 'x' is predicated as 'Cxtα', and this variable 'x' is bound by '∀x' over the whole formula).
Ambiguity
The English word 'ambiguity' comes from Latin 'ambigere' or ambigō,12 meaning 'to dispute', 'to be undecided' and 'to call in question'.13 'Ambigō is a compound word consisting of 'ambi' and 'agō' (or 'agere' in the case of 'ambigere'). 'Ambi' has the same meaning as its Greek root 'amphi',14 namely 'around' or 'about'.15 It is also related to the Greek 'ampho' and 'amphis', meaning 'both' and 'both sides'.16 And 'agō', meaning 'to drive',17 has a similar meaning as its Greek root 'āgo',18 and its Sanskrit root 'ājati'.19 Thus does ambiguity drive one around to more than one side. So when in logic one sentence can be interpreted in more than one legitimate manner, then that sentence is ambiguous.20 And the capitalistic slogan is logically ambiguous because it can logically be interpreted and formulated in more than one manner. For in the previous paragraph two very different logical interpretations and translations were given.
Now without intending to pone a complete theory of ambiguity can three different types of ambiguity be discerned. In the first type of ambiguity all possible interpretations are unhidden. An example of such a sentence is 'Sein und Zeit is Heidegger's best known work'. This sentence may say that Sein und Zeit is known best among all of Heidegger's works, and it may say that Sein und Zeit is the best among all of Heidegger's known works. Both interpretations are seen at once or very quickly, and thus may both interpretations be considered to be unhidden.
In the second type of ambiguity not all possible interpretations are unhidden. Some possible interpretations are hidden. An example of this type of ambiguity is the sentence 'Arthur Schopenhauer wanted to be the most popular philosopher of his time'. When hearing or reading this sentence one will instantly interpret that Schopenhauer wanted that he himself would be referred to as the most popular philosopher of his time. A hidden interpretation however may also say that Schopenhauer wanted to be Georg Wilhelm Friedrich Hegel, who at Schopenhauer's time was the most popular philosopher. In this example the first interpretation can be considered to be unhidden and the second interpretation can be considered to be hidden. The first interpretation comes up instantly with such a clarity that the second one does not even spring to mind.
In the third type of ambiguity all interpretations are hidden. An example of such a type of ambiguity is the sentence 'the smurf smurfed a smufeous smurf'. No interpretation comes up when hearing or reading this sentence. All interpretations remain hidden.
It should be added that whether an ambiguity is of the first, second or third kind will also depend on the interpreter. Probably few interpretations will stay hidden for an excellent logician, philosopher, linguist or judge. However with the general plain users of language in mind a non-strict classification of ambiguous sentences along the above lines may be made.
Now the question may rise how the capitalistic slogan may be classified. This slogan was enunciated as; 'in capitalism everybody has the chance to be successful'. Because two different messages are conveyed by this slogan it is ambiguous. And since one message is more dominantly present than the other can this slogan be classified as belonging to the second type of ambiguity. One message in the capitalistic slogan is more hidden than the other.
The message which is the most unhidden of the two is expressed by formula 1. This formula asserts that it is necessary for every being at every point in time that if this being is human then it is so that if he lives in a capitalistic system at a certain point in time then it is possible that he is successful at that point in time. And this assertion implies, as we have deduced and seen, that if one human in a capitalistic system has the possibility for success then all such humans must have that possibility at the same time.
The second message in the capitalistic slogan is the one which stays the most hidden of the two. This message is expressed by formula 2, which asserts that it is necessary for every being at every point in time that if this being is human then it is so that if he lives in a capitalistic system at a certain point in time then it is possible that there is a being who is successful at that point in time and that that being is the human who is placed in the capitalistic society. This formula expresses an individuality of the possibility to be successful, whereas the other formula expresses a universality of that possibility.
Thus when people unthoughtfully use the capitalistic slogan to defend the capitalistic system, then they convey one message of the slogan but hide another.
Truth Values
Now with the capitalistic slogan a little bit elucidated in the previous paragraphs it may be asked which one of the two meanings is more valid. That messages may be more hidden in ambiguous sentences is generally not much of a problem if those messages are also less valid. In an ambiguous sentence of the second type the most valid assertion should be the most unhidden one. This consideration then leads automatically to the question which of the two assertions in the capitalistic slogan is the most valid one. To come to a determination of this we shall make use of truth tables. To come to a decision through these truth tables three concrete examples must be taken. One example must be a person in capitalism who has been successful throughout his life. One example must be a person in capitalism who has had unsuccessful and successful periods in his life. And one example must be a person in capitalism who has been unsuccessful throughout his life. In the forementioned order we shall take as examples Juliana van Oranje-Nassau (1909-2004), queen of the Netherlands, Milton Friedman (1912-2006), American economist, and Maxi Linder (1902-1981), a Surinam prostitute who never reached success during her life. We shall take two points in time. As the first point in time the birth time of Milton Friedman on 31 July 1912 shall be taken. Born in a working class family he wasn't born successful. Van Oranje-Nassau, born in a royal family, was successful from birth, and Linder, being born unsuccessful, stayed so throughout her life. As second point in time we shall take the time that Friedman was awarded the Nobel prize in economics, (named officially 'The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel') on 14 October 1976. At that time obviously van Oranje-Nassau was still successful and Linder still wasn't. In the truth table queen Juliana van Oranje-Nassau shall be symbolized with 'o', Milton Friedman with 'f' and Maxi Linder with 'l'. The first point in time shall be symbolized with 't1' and the second with 't2'. In the tables '1' will stand for 'true' and '0' will stand for 'untrue'. If the truth value cannot be determined a question mark shall be filled in.
So let's have a look at the truth table of the first formula. With help of the earlier executed deconstruction we may come to the following table.
| Ho | 1 |
| Hf | 1 |
| Hl | 1 |
| Cot1 | 1 |
| Cot2 | 1 |
| Cft1 | 1 |
| Cft2 | 1 |
| Clt1 | 1 |
| Clt2 | 1 |
| Sot1 | 1 |
| Sot2 | 1 |
| Sft1 | 0 |
| Sft2 | 1 |
| Slt1 | 0 |
| Slt2 | 0 |
| ◊Sot1 | 1 |
| ◊Sot2 | 1 |
| ◊Sft1 | ? |
| ◊Sft2 | 1 |
| ◊Slt1 | ? |
| ◊Slt2 | ? |
| Cot1⇒◊Sot1 | 1 |
| Cot2⇒◊Sot2 | 1 |
| Cft1⇒◊Sft1 | ? |
| Cft2⇒◊Sft2 | 1 |
| Clt1⇒◊Slt1 | ? |
| Clt2⇒◊Slt2 | ? |
| Ho⇒(Cot1⇒◊Sot1) | 1 |
| Ho⇒(Cot2⇒◊Sot2) | 1 |
| Hf⇒(Cft1⇒◊Sft1) | ? |
| Hf⇒(Cft2⇒◊Sft2) | 1 |
| Hl⇒(Clt1⇒◊Slt1) | ? |
| Hl⇒(Clt2⇒◊Slt2) | ? |
| ∀tα(Ho⇒(Cotα⇒◊Sotα)) | 1 |
| ∀tα(Hf⇒(Cftα⇒◊Sftα)) | ? |
| ∀tα(Hl⇒(Cltα⇒◊Sltα)) | ? |
| ∀x∀tα(Hx⇒(Cxtα⇒◊Sxtα)) | ? |
| □∀x∀tα(Hx⇒(Cxtα⇒◊Sxtα)) | ? |
As the calculations in the truth table show is it with the given data not possible to decide upon the truth value of formula 1. Let's have a look at what the outcome will be for formula 2 when we calculate its truth value in a truth table.
| Ho | 1 |
| Hf | 1 |
| Hl | 1 |
| Cot1 | 1 |
| Cot2 | 1 |
| Cft1 | 1 |
| Cft2 | 1 |
| Clt1 | 1 |
| Clt2 | 1 |
| Sot1 | 1 |
| Sot2 | 1 |
| Sft1 | 0 |
| Sft2 | 1 |
| Slt1 | 0 |
| Slt2 | 0 |
| ∃y(Syt1∧o=y) | 1 |
| ∃y(Syt2∧o=y) | 1 |
| ∃y(Syt1∧f=y) | 0 |
| ∃y(Syt2∧f=y) | 1 |
| ∃y(Syt1∧l=y) | 0 |
| ∃y(Syt2∧l=y) | 0 |
| ◊(∃y(Syt1∧o=y)) | 1 |
| ◊(∃y(Syt2∧o=y)) | 1 |
| ◊(∃y(Syt1∧f=y)) | ? |
| ◊(∃y(Syt2∧f=y)) | 1 |
| ◊(∃y(Syt1∧l=y)) | ? |
| ◊(∃y(Syt2∧l=y)) | ? |
| Cot1⇒◊(∃y(Syt1∧o=y)) | 1 |
| Cot2⇒◊(∃y(Syt2∧o=y)) | 1 |
| Cft1⇒◊(∃y(Syt1∧f=y)) | ? |
| Cft2⇒◊(∃y(Syt2∧f=y)) | 1 |
| Clt1⇒◊(∃y(Syt1∧l=y)) | ? |
| Clt2⇒◊(∃y(Syt2∧l=y)) | ? |
| Ho⇒(Cot1⇒◊(∃y(Syt1∧o=y))) | 1 |
| Ho⇒(Cot2⇒◊(∃y(Syt2∧o=y))) | 1 |
| Hf⇒(Cft1⇒◊(∃y(Syt1∧f=y))) | ? |
| Hf⇒(Cft2⇒◊(∃y(Syt2∧f=y))) | 1 |
| Hl⇒(Clt1⇒◊(∃y(Syt1∧l=y))) | ? |
| Hl⇒(Clt2⇒◊(∃y(Syt2∧l=y))) | ? |
| ∀tα(Ho⇒(Cotα⇒◊(∃y(Sytα∧o=y)))) | 1 |
| ∀tα(Hf⇒(Cftα⇒◊(∃y(Sytα∧f=y)))) | ? |
| ∀tα(Hl⇒(Cltα⇒◊(∃y(Sytα∧l=y)))) | ? |
| ∀x∀tα(Hx⇒(Cxtα⇒◊(∃y(Sytα∧x=y)))) | 1 |
| □∀x∀tα(Hx⇒(Cxtα⇒◊(∃y(Sytα∧x=y)))) | 1 |
The calculations in this second truth table show that formula 2 is valid.
Conclusion
In this contemplation we set out to logically refute the capitalistic slogan. For this the slogan first needed to be explored. This was done in the first paragraph where the slogan was brought to the fore as 'in capitalism everybody has the chance to be successful'. After a very short introduction in modal first order predicate logic in the second paragraph was the capitalistic slogan logically formulated in the third paragraph. Two formulas were found. The first formula, '□∀x∀tα(Hx⇒(Cxtα⇒◊Sxtα))', asserts that it is necessary for every being at every point in time that if this being is human then it is so that if he lives in a capitalistic system at a certain point in time then it is possible that he is successful at that point in time. This formula implies that if one human in a capitalistic system has the possibility for success then all such humans must have that possibility at the same time. The second formula, '□∀x∀tα(Hx⇒(Cxtα⇒◊(∃y(Sytα∧x=y))))', asserts that it is necessary for every being at every point in time that if this being is human then it is so that if he lives in a capitalistic system at a certain point in time then it is possible that there is a being who is successful at that point in time and that that being is the human who is placed in the capitalistic society. That two logical formulas could be given for the capitalistic slogan meant that this slogan was ambiguous. This ambiguity was explored in the fourth paragraph. The capitalistic slogan was classified as belonging to the second type of ambiguity. The logical meaning of formula 1 is more unhidden than that of formula 2. Thus in the fifth paragraph the truth values of both formulas were calculated. It turned out that the truth value of formula 1 cannot be determined on base of the used data, whereas formula 2 with that data can be determined to be true.
The above must bring us to the conclusion that the capitalistic slogan hides its valid message under an unhidden message of which the validity cannot be determined. With this it posits itself in a dubious position. For as far as the capitalistic slogan conveys the meaning of formula 2 its use is legitimate. However in conveying the meaning of formula 1 the legitimacy of its use is very questionable. Basically the capitalistic slogan uses its valid meaning to legitimate its use, but at the same time conveys a very questionable meaning. In the capitalistic slogan truth is used for the purpose of conveying what might very well be untruth. But this is an utter deceit. The capitalistic slogan is definitely of a deceitful nature and must thus be forcefully refuted. May this be the action of all who contemplate the capitalistic slogan along logical lines.
Notes
- Oxford English Dictionary, Second Edition on CD-ROM (v. 4.0), Oxford University Press, 2009, capitalism.
- Ibidem, capitalist.
- John Ayto, Word Origins, The Hidden Histories of English Words from A to Z, A & C Black, London, 2005, p. 462.
- Milton Friedman and Rose Friedman, Free to Choose, A Personal Statement, Harcourt Brace Jovanovich, New York / London, 1980, p. 146. "Wherever the free market has been permitted to operate, wherever anything approaching equality of opportunity has existed, the ordinary man has been able to attain levels of living never dreamed of before."
- Roy T. Cook, A Dictionary of Philosophical Logic, Edinburgh University Press, Edinburgh, 2009, p. 174.
- Ibidem, p. 264.
- Ibidem, p. 226.
- Ibidem, p. 236-237.
- Ibidem, p. 176.
- Ibidem, p. 191.
-
1. □∀x∀tα(Hx⇒(Cxtα⇒◊Sxtα)) ass 2. □∀tα(Ha⇒(Catα⇒◊Satα)) E∀1 3. □∃y∀tα(Hy⇒(Cytα⇒◊Sytα)) I∃2 4. □∃y∀tα(Hy⇒(Cytα⇒◊Sytα)) 3 5. □∀x∀tα(Hx⇒(Cxtα⇒◊Sxtα)) 1 6. □∃y∀tα(Hy⇒(Cytα⇒◊Sytα)) ⇒ □∀x∀tα(Hx⇒(Cxtα⇒◊Sxtα)) I⇒4, 5 - Word Origins, p. 22.
- Oxford Latin Dictionary, Oxford University Press, London, 1968, p. 113.
- Ibidem.
- Francis Edward Jackson Valpy, The Etymology of Words of the Greek Language, In Alphabetical Order, With the Omission Generally of Plants and Sometimes of the More Uncommon Animals, Longman, Green, Longman and Roberts, London, 1860, p. 11.
- Ibidem.
- Oxford Latin Dictionary, p. 87.
- The Etymology of Words of the Greek Language, p. 3.
- Monier Williams, A Sanskrit-English Dictionary, Etymologically and Philologically Arranged, With Special Reference to Greek, Latin, Gothic, German, Anglo-Saxon, and Other Cognate Indo-European Languages, The Clarendon Press, Oxford, p. 115, āj.
- A Dictionary of Philosophical Logic, p. 11.
Bibliography
- John Ayto, Word Origins, The Hidden Histories of English Words from A to Z, A & C Black, London, 2005.
- Roy T. Cook, A Dictionary of Philosophical Logic, Edinburgh University Press, Edinburgh, 2009.
- Milton Friedman and Rose Friedman, Free to Choose, A Personal Statement, Harcourt Brace Jovanovich, New York / London, 1980.
- Francis Edward Jackson Valpy, The Etymology of Words of the Greek Language, In Alphabetical Order, With the Omission Generally of Plants and Sometimes of the More Uncommon Animals, Longman, Green, Longman and Roberts, London, 1860.
- Monier Williams, A Sanskrit-English Dictionary, Etymologically and Philologically Arranged, With Special Reference to Greek, Latin, Gothic, German, Anglo-Saxon, and Other Cognate Indo-European Languages, The Clarendon Press, Oxford.
- Oxford English Dictionary, Second Edition on CD-ROM (v. 4.0), Oxford University Press, 2009.
- Oxford Latin Dictionary, Oxford University Press, London, 1968.