- Titel: Contemplaties, Een logische refutatie van de kapitalistische slogan.
- Auteur: Arvindus.
- Uitgever: Arvindus.
- Auteursrecht: Arvindus, 2010, alle rechten voorbehouden.
- Index: 201006052.
- Editie: html, first editie.
- Origineel: Contemplations, A Logical Refutation of the Capitalistic Slogan, Index: 201006051.
Inleiding
Voor een actie op een onderwerp verricht kan worden moet een idee van dat onderwerp worden gevormd. En hoe helderder het gevormde idee is hoe accurater de actie verricht kan worden. Dus wanneer de actie van een logische refutatie verricht gaat worden op het onderwerp van de kapitalistische slogan moet eerst een helder idee van die laatste worden gevorm. Aldus zullen we deze contemplatie starten met een korte exploratie van de kapitalistische slogan. Na helderheid over dit onderwerp te hebben verkregen kan het logisch gerefuteerd worden.
De kapitalistische slogan
Om de kapitalistische slogan te verhelderen en expliceren dient eerst een idee gevormd te worden over wat kapitalisme is. Nu is er veel geschreven en gezegd over kapitalisme, zowel door voorstanders als tegenstanders. Over het algemeen lijken beide partijen het eens te zijn over wat kapitalisme is, maar daarna scheiden hun wegen. Hun verdere argumenten bestaan dan veelal uit de voors en tegens van het systeem. Met deze zullen we niet veel van doen hebben in deze contemplatie. Wat onze interesse echter wekt is het antwoord op de vraag waar beide partijen mee instemmen over wat kapitalisme is. Hun wederzijdse conclusies hierover worden weerspiegeld en kortbondig geformuleerd in het Engelse woordenboek. Volgens het woordenboek is kapitalisme een systeem dat het bestaan van kapitalisten voorstaat.1 En een kapitalist op zijn beurt wordt in het woordenboek beschouwd iemand te zijn die kapitaal heeft verzameld of iemand die kapitaal beschikbaar heeft voor emplooiing in financiële of industriële ondernemingen.2 Aldus is kapitalisme een systeem dat het bestaan van personen voorstaat die kapitaal hebben verzameld dat beschikbaar is voor emplooing in ondernemingen. Dit woord 'empooiing' (ook beschouwbaar als neologisme dat is afgeleid van de Nederlandse woorden 'emplooi' en 'ontplooiing' en het Engelse 'employment') is ambigu in deze context. Het maakt dat 'kapitaal' kan refereren aan kapitaal dat beschikbaar is voor investering in ondernemingen of aan kapitaal dat beschikbaar is om werkers in te huren bij ondernemingen. In dit geval maakt de ambiguïteit niet veel uit omdat hier beide lezingen valide zijn. Kapitalisme is een systeem dat het bestaan voorstaat van personen die kapitaal verzameld hebben dat beschikbaar is voor investering in, en inhuren van werkers voor financiële of industriële ondernemingen.
Wat wordt dan bedoeld met 'de kapitalistische slogan'? We zijn gekomen tot een idee van wat kapitalisme is en nu moet een idee gevormd worden van wat een slogan is. Na zulk idee verkregen te hebben kunnen beide ideeën opnieuw samengenomen worden in hun heelheid van de kapitalistische slogan. Wat is dus een slogan? Het woord komt van het Gallische 'sluaghghairm', betekenend 'strijdkreet'.3 Een strijd nu wordt gevochten voor ofwel verdediging ofwel aanval en vergelijkbaar zijn slogans linguïstische expressies die gebruikt worden om te verdedigen of aan te vallen. Wat de kapitalistische slogan probeert te verdedigen is natuurlijk kapitalisme en wat het probeert aan te vallen zijn de vijanden van kapitalisme. De strijd van kapitalisme wordt linguïstisch ook gevochten op meer intellectuele niveaus zoals in lange verhandelingen. Het is van deze intellectuele verhandelingen dat frasen onttrokken worden om de in de verhandelingen gepresenteerde ideeën samen te vatten. Zulke frasen bewegen van de ene persoon naar de andere, de ideeën op een zeer summiere manier presenterend. Uiteindelijk worden ze publieke slogans, herkend in hun geworteldheid door sommigen maar als zodanig onherkend door velen. De kapitalistische slogan zoals bedoeld in deze contemplatie is nu geworteld in het idee dat in het kapitalistische systeem iedereen de kans heeft om een hoge standaard van welzijn te bereiken.4 En dit kapitalistische idee wordt samengevat in een frase die de kapitalistische slogan is geworden. Deze slogan en strijdkreet, onbedachtzaam gebruikt door vele pro-kapitalisten, klinkt ongeveer als volgt: 'in kapitalisme heeft iedereen de kans om succesvol te zijn'.
Modale eerste-orde-predicaten-logica
Voor onze logische refutatie van de kapitalistische slogan zullen we gebruik maken van modale eerste-orde-predicaten-logica. Logica structureert argumenten om te beslissen over hun accepteerbaarheid of hun niet-accepteerbaarheid.5 Modale eerste-orde-predicaten-logica doet dit door de onderwerpen, predicaten, kwantificatoren, conjuncties en modaliteiten die aanwezig kunnen zijn in een argument te expliceren, en het expliceert deze door middel van symbolen. Onderwerpen (in logica 'singuliere termen' genaamd) worden gesymboliseerd met kleine letters (a, b, c, ..., in geval van constanten, …, x, y, z, in geval van variabelen).6 De antiek filosoof 'Socrates' kan bijvoorbeeld gesymboliseerd worden met 's'. Of het tijdstip '14 februari 2010, 8/30 PM CET' kan bijvoorbeeld gesymboliseerd worden met 't1'. Predicaten worden gesymboliseerd met hoofdletters (A, B, C, …).7 En zoals predicaten in zinnen tot onderwerpen behoren zo worden ook de symbolen logisch samen geschreven. De bewering 'Immanuel Kant ging voor een wandeling op 14 februari 1783 om 5.00 PM CET' kan bijvoorbeeld gesymboliseerd worden als 'Wkt1'. Kwantificatoren worden gesymboliseerd door de symbolen '∀' en '∃'.8 Wanneer de universele kwantificator '∀' wordt gebruikt in een logische formule duidt dit aan dat de bewering die deze kwantificator volgt valide is voor alle bestaanden die hij bindt. Bijvoorbeeld een formule zoals '∀xFx' kan beweren dat alle bestaanden eindig zijn. De existentiële kwantificator '∃' wordt gebruikt om het bestaan van minstens één bestaande aan te duiden. Een formule zoals '∃xHx' kan beweren dat er een bestaande is die menselijk is. Connectieven worden gesymboliseerd door wiskundige symbolen zoals '∧', '∨', '⇒', '⇔' en '¬'.9 Deze connectieven verbinden onderwerpen, geprediceerde onderwerpen en samengestelde formules. Van deze connectieven staat '∧' voor '… en …', staat '∨' voor '… of …', staat '⇒' voor 'als … dan …', staat '⇔' voor '… is gelijk aan …' en staat '¬' voor 'het is niet zo dat …'. Bijvoorbeeld de formule '¬Fs⇒¬Hs' kan beweren dat als het niet zo is dat Socrates eindig is dat hij dan geen mens is. Het welbekende gelijkheidssymbool '=' wordt ook gebruikt als een connectief om een identiteit te indiceren. Andere gebruikte wiskundige symbolen zijn haakjes, die een vergelijkbare functie hebben in modale eerste orde predicaten logica als in wiskunde. De logische functie die geplaatst wordt net voor de haakjes is valide voor het geheel van de formule die geplaatst is binnen de haakjes. De formule '∃x(Fx∧x=s)' kan beweren dat er een bestaande is dat eindig is en dat die bestaande Socrates is. Als conclusie van deze zeer korte introductie in modale eerste orde predicaten logica zullen twee modaliteitssymbolen gegeven worden. Deze betreffen de symbolen voor 'noodzakelijk' en 'mogelijk', namelijk '□' en '◊'.10 De formule '□∀x(Hx⇒Fx)' kan beweren dat het noodzakelijk is voor alle bestaanden dat als ze mens zijn dat ze eindig zijn.
Principiële formules
Laten we nu dan deze modale eerste-orde-predicaten-logica toepassen op de kapitalistische slogan. Deze slogan werd verkondigd als: 'in kapitalisme heeft iedereen de kans om succesvol te zijn'. Alvorens een logische formulering mogelijk is moeten eerst het domein en de vertaalsleutels bepaald worden. Als domein zullen we alle wezens nemen (a, b, c, …) en alle tijdstippen (t1, t2, t3, …). De vertalingssleutels hebben we als volgt bepaald. 'C' staat voor '…leeft in een kapitalistisch systeem op tijdstip…'. 'S' staat voor '…is succesvol op tijdstip…'. En 'H' staat voor '…is menselijk'.
Met het domein en predicaten nu gedefinieerd zijn we in staat om de kapitalistische slogan als volgt te formuleren.
1) □∀x∀tα(Hx⇒(Cxtα⇒◊Sxtα))
Deze formule beweert dat het noodzakelijk is voor elk wezen op elk tijdstip dat als dit wezen mens is het zo is dat als hij leeft in een kapitalistisch systeem op een bepaald tijdstip het mogelijk is dat hij succesvol is op dat tijdstip.
Een deconstructie van deze formule zal tonen hoe deze gestructureerd en opgebouwd is.
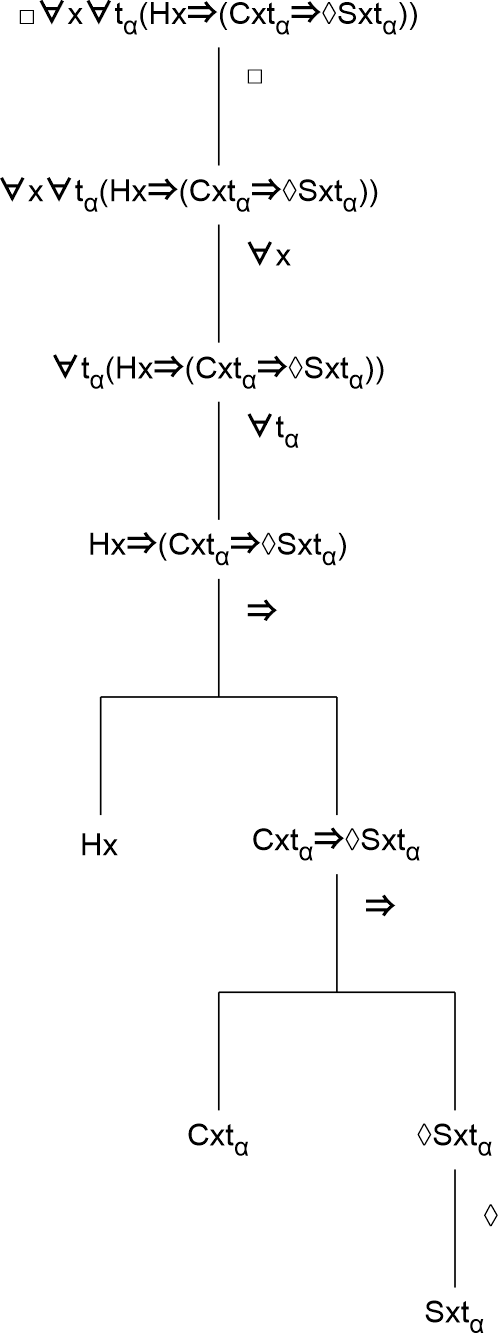
Wat deze deconstructie onder andere toont is dat de subformule 'Sxtα' gebonden wordt door de universele kwantificatoren '∀x' en '∀tα'. Dit betekent dat als een actualisatie van de mogelijkheid van succesvol zijn plaatsvindt op een bepaalde tijd (en deze mogelijkheid wordt uitgedrukt door de subformule '◊Sxtα'), dat dit zal plaatsvinden voor alle mensen die in een kapitalistisch systeem leven op dat tijdstip (dat laatste volgens de subformule 'Cxtα' die ook gebonden wordt door '∀x' en '∀tα'). Aldus impliceert deze formule dat als één mens in een kapitalistisch systeem de mogelijkheid op succes heeft dat dan alle zulke mensen die mogelijkheid moeten hebben op dezelfde tijd.11 Allen worden succesvol of niemand wordt succesvol.
Echter de kapitalistische slogan brengt niet noodzakelijk de logische boodschap over dat alle mensen die in een kapitalistische maatschappij leven de mogelijkheid hebben om succesvol te zijn op hetzelfde tijdstip. Deze kan ook beweren dat van alle mensen die in een kapitalistische samenleving leven slechts één of enkelen de mogelijkheid hebben om succesvol te zijn op hetzelfde tijdstip en dat die ene of die enkelen iedereen kunnen zijn. Dit is wat de volgende formule beweert.
2) □∀x∀tα(Hx⇒(Cxtα⇒◊(∃y(Sytα∧x=y))))
Deze formule beweert dat het noodzakelijk is voor elk wezen op elk tijdstip dat als dit wezen mens is dat het zo is dat als hij in een kapitalistische samenleving leeft op een bepaald tijdstip het mogelijk is dat er een wezen is dat succesvol is op dat tijdstip en dat dat wezen die mens is die geplaatst is in de kapitalistische samenleving. Deze formule kan gedeconstrueerd worden als volgt.
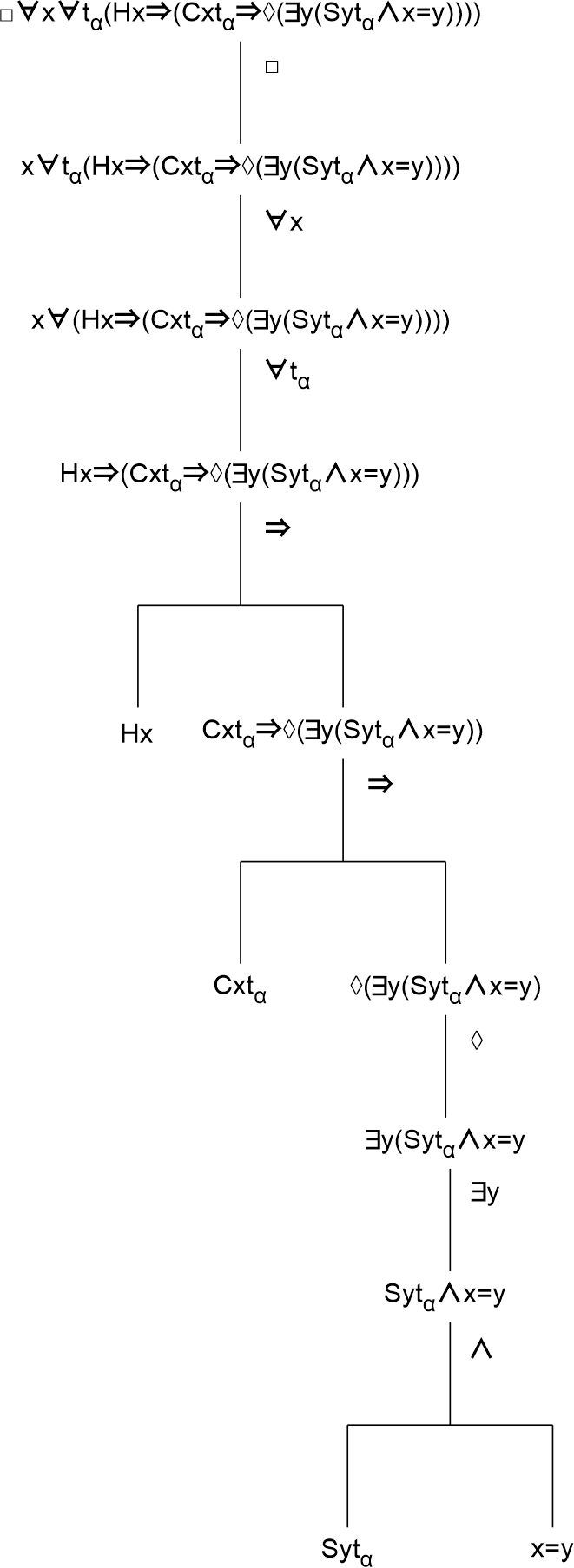
Deze deconstructie toont dat de subformule 'Sytα' gebonden wordt door de existentiële kwantificator '∃y'. Dit toont alreeds dat een actualisatie van de mogelijkheid van succesvol zijn niet plaats zal vinden voor alle mensen op hetzelfde tijdstip. Maar wat geactualiseerd kan worden is de subformule die gebonden wordt door de modale mogelijkheidsfunctie '◊', en dit betreft de subformule '∃ySytα∧x=y'. Hier drukt '∃ySytα' de individualiteit van de mens of de mensen uit die succesvol kunnen zijn. En 'x=y' drukt uit dat deze mens of deze mensen behoren tot degenen levend in een kapitalistisch system (omdat 'x' als 'Cxtα' geprediceerd wordt, en deze variabele 'x' wordt gebonden door '∀x' over de gehele formule).
Ambiguïteit
Het Nederlandse woord 'ambiguïteit' komt (in lijn met het Engelse 'ambiguity') van het Latijnse 'ambigere' of ambigō,12 betekenend 'betwisten', 'onbesloten zijn' en 'in vraag stellen'.13 'Ambigō is een samengesteld woord bestaande uit 'ambi' en 'agō' (of 'agere' in geval van 'ambigere'). 'Ambi' heeft dezelfde betekenis als zijn Griekse wortel 'amphi',14 namelijk 'rond' of 'om'.15 Het is ook gerelateerd aan het Griekse 'ampho' en 'amphis', betekenend 'beide' en 'beide zijden'.16 En 'agō', betekenend 'drijven',17 heeft een vergelijkbare betekenis in zijn Griekse wortel 'āgo',18 en zijn Sanskriet wortel 'ājati'.19 Aldus drijft ambiguïteit iemand rond naar meer dan één zijde. Dus wanneer in logica één zin op meer dan één legitieme manier geïnterpreteerd kan worden dan is die zin ambigu.20 En de kapitalistische slogan is logisch ambigu omdat het logisch geïnterpreteerd en geformuleerd kan worden op meer dan één manier. Want in de vorige paragraaf werden twee zeer verschillende logische interpretaties en vertalingen gegeven.
Zonder nu de intentie te hebben om een complete theorie van ambiguïteit te poneren kunnen drie verschillende typen van ambiguïteit onderscheiden worden. In het eerste type ambiguïteit zijn alle mogelijke interpretaties onverborgen. Een voorbeeld van zulk een zin is 'Sein und Zeit is Heidegger's beste bekende werk'. Deze zin kan zeggen dat Sein und Zeit het beste bekend is onder al Heidegger's werken en het kan zeggen dat Sein und Zeit onder al Heidegger's bekende werken het beste is. Beide interpretaties worden onmiddellijk gezien of zeer snel, en dus kunnen beide interpretaties beschouwd worden onverborgen te zijn.
In het tweede type ambiguïteit zijn niet alle mogelijk interpretaties onverborgen. Sommige mogelijke interpretaties zijn verborgen. Een voorbeeld van dit type van ambiguïteit is de zin 'Arthur Schopenhauer wilde de meest populaire filosoof van zijn tijd zijn'. Wanneer deze zin gehoord of gelezen wordt zal men onmiddellijk interpreteren dat Schopenhauer wilde dat aan hemzelf gerefereerd zou worden als de meest populaire filosoof van zijn tijd. Een verborgen interpretatie echter kan ook zeggen dat Schopenhauer Georg Wilhelm Friedrich Hegel wilde zijn, die tijdens Schopenhauer's tijd de meest populaire filosoof was. In dit voorbeeld kan de eerste interpretatie beschouwd worden onverborgen te zijn en de tweede interpretatie kan beschouwd worden verborgen te zijn. De eerste interpretatie komt onmiddellijk op met zulk een duidelijkheid dat de tweede niet eens in het denken opkomt.
In het derde type ambiguïteit zijn alle interpretaties verborgen. Een voorbeeld van zulk een type ambiguïteit is de zin 'de smurf smurfde een smurfelijke smurf'. Geen interpretatie komt op wanneer deze zin gehoord of gelezen wordt. Alle interpretaties blijven verborgen.
Er moet toegevoegd worden dat of een ambiguïteit van de eerste, tweede of derde aard is ook zal afhangen van de interpreteerder. Waarschijnlijk weinig interpretaties zullen verborgen blijven voor een uitstekend logicus, taalkundige of rechter. Echter met de algemene gewone gebruikers van taal in gedachte kan een niet-strikte classificatie van ambigue zinnen volgens bovenstaande lijnen gemaakt worden.
Nu kan de vraag rijzen hoe de kapitalistische slogan geclassificeerd kan worden. Deze slogan werd geformuleerd als; 'in kapitalisme heeft iedereen de kans om succesvol te zijn'. Omdat twee verschillende boodschappen worden overgebracht door deze slogan is hij ambigu. En aangezien één boodschap dominanter aanwezig is dan de ander kan deze slogan geclassificeerd worden als behorend tot het tweede type ambiguïteit. De ene boodschap is in de kapitalistische slogan meer verborgen dan de andere.
De boodschap die het meest onverborgen is van de twee wordt uitgedrukt door formule 1. Deze formule beweert dat het noodzakelijk is voor elk wezen op elk tijdstip dat als dit wezen mens is het zo is dat als hij leeft in een kapitalistisch systeem op een bepaald tijdstip het mogelijk is dat hij succesvol is op dat tijdstip. En deze bewering impliceert, zoals we hebben gededuceerd en gezien, dat als één mens in een kapitalistisch systeem de mogelijkheid op succes heeft dat dan al zulke mensen die mogelijkheid moeten hebben op dezelfde tijd.
De tweede boodschap in de kapitalistische slogan is degene die het meest verborgen blijft van de twee. Deze boodschap wordt uitgedrukt door formule 2, die beweert dat het noodzakelijk is voor elk wezen op elk tijdstip dat als dit wezen mens is dat het zo is dat als hij in een kapitalistische samenleving leeft op een bepaald tijdstip het mogelijk is dat er een wezen is dat succesvol is op dat tijdstip en dat dat wezen die mens is die geplaatst is in de kapitalistische samenleving. Deze formule drukt een individualiteit van de mogelijkheid om succesvol te zijn uit, terwijl de andere formule een universaliteit van die mogelijkheid uitdrukt.
Wanneer mensen aldus onbedachtzaam de kapitalistische slogan gebruiken om het kapitalistisch systeem te verdedigen dan brengen zij één boodschap van de slogan over maar verbergen ze een andere.
Waarheidswaarden
Met de kapitalistische slogan nu een beetje verhelderd in de vorige paragrafen kan gevraagd worden welk van de twee betekenissen meer valide is. Dat boodschappen meer verborgen kunnen zijn in ambigue zinnen is over het algemeen geen groot probleem als deze boodschappen ook minder valide zijn. In een ambigue zin van het tweede type zou de meest valide bewering ook de meest onverborgen moeten zijn. Deze beschouwing leidt dan automatisch naar de vraag welk van de twee beweringen in de kapitalistische slogan de meest valide is. Om tot een bepaling hiervan te komen zullen we gebruik maken van waarheidstabellen. Om te komen tot een beslissing via deze waarheidstabellen moeten drie concrete voorbeelden gegeven worden. Eén voorbeeld moet een persoon in kapitalisme zijn die zijn gehele leven succesvol is geweest. Eén voorbeeld moet een persoon in kapitalisme zijn die onsuccesvolle en succesvolle perioden in zijn leven heeft gehad. En één voorbeeld moet een persoon in kapitalisme zijn die zijn gehele leven onsuccesvol is geweest. In de voorgenoemde volgorde zullen Juliana van Oranje-Nassau (1909-2004), koningin van Nederland, Milton Friedman (1912-2006), Amerikaans econoom, en Maxi Linder (1902-1981), een Surinaamse prostitué die nooit succes bereikte gedurende haar leven, genomen worden. We zullen twee tijdstippen nemen. Als eerste tijdstip zal de geboortetijd van Milton Friedman op 31 juli 1912 genomen worden. Geboren in een arbeidersklassefamilie werd hij niet succesvol geboren. Van Oranje-Nassau, geboren in een koninklijke familie, was succesvol vanaf de geboorte, en Linder, onsuccesvol geboren, bleef dit doorheen haar leven. Als tweede tijdstip zullen we het tijdstip nemen waarop Friedman beloond werd met de Nobelprijs in economie, (officieel genoemd 'De Sveriges Riksbank Prijs in Economische Wetenschappen in Herinnering aan Alfred Nobel') op 14 oktober 1976. Op dat tijdstip was van Oranje-Nassau vanzelfsprekend nog steeds succesvol en Linder nog steeds niet. In de waarheidstabel zal koningin Juliana van Oranje-Nassau gesymboliseerd worden met 'o', Milton Friedman met 'f' en Maxi Linder met 'l'. Het eerste tijdstip zal gesymboliseerd worden met 't1' en het tweede met 't2'. In de tabellen zal '1' staan voor 'waar' en '0' staan voor 'onwaar'. Wanneer de waarheidswaarde niet bepaald kan worden zal een vraagteken ingevuld worden.
Laten we dus een kijk nemen op de waarheidstabel van de eerste formule. Met behulp van de eerder uitgevoerde deconstructie kunnen we komen tot de volgende tabel.
| Ho | 1 |
| Hf | 1 |
| Hl | 1 |
| Cot1 | 1 |
| Cot2 | 1 |
| Cft1 | 1 |
| Cft2 | 1 |
| Clt1 | 1 |
| Clt2 | 1 |
| Sot1 | 1 |
| Sot2 | 1 |
| Sft1 | 0 |
| Sft2 | 1 |
| Slt1 | 0 |
| Slt2 | 0 |
| ◊Sot1 | 1 |
| ◊Sot2 | 1 |
| ◊Sft1 | ? |
| ◊Sft2 | 1 |
| ◊Slt1 | ? |
| ◊Slt2 | ? |
| Cot1⇒◊Sot1 | 1 |
| Cot2⇒◊Sot2 | 1 |
| Cft1⇒◊Sft1 | ? |
| Cft2⇒◊Sft2 | 1 |
| Clt1⇒◊Slt1 | ? |
| Clt2⇒◊Slt2 | ? |
| Ho⇒(Cot1⇒◊Sot1) | 1 |
| Ho⇒(Cot2⇒◊Sot2) | 1 |
| Hf⇒(Cft1⇒◊Sft1) | ? |
| Hf⇒(Cft2⇒◊Sft2) | 1 |
| Hl⇒(Clt1⇒◊Slt1) | ? |
| Hl⇒(Clt2⇒◊Slt2) | ? |
| ∀tα(Ho⇒(Cotα⇒◊Sotα)) | 1 |
| ∀tα(Hf⇒(Cftα⇒◊Sftα)) | ? |
| ∀tα(Hl⇒(Cltα⇒◊Sltα)) | ? |
| ∀x∀tα(Hx⇒(Cxtα⇒◊Sxtα)) | ? |
| □∀x∀tα(Hx⇒(Cxtα⇒◊Sxtα)) | ? |
Zoals de berekeningen in de waarheidstabel tonen is het met de gegeven data niet mogelijk om te beslissen over de waarheidswaarde van formule 1. Laten we kijken wat de uitkomst zal zijn voor formule 2 wanneer we zijn waarheidswaarde berekenen in een waarheidstabel.
| Ho | 1 |
| Hf | 1 |
| Hl | 1 |
| Cot1 | 1 |
| Cot2 | 1 |
| Cft1 | 1 |
| Cft2 | 1 |
| Clt1 | 1 |
| Clt2 | 1 |
| Sot1 | 1 |
| Sot2 | 1 |
| Sft1 | 0 |
| Sft2 | 1 |
| Slt1 | 0 |
| Slt2 | 0 |
| ∃y(Syt1∧o=y) | 1 |
| ∃y(Syt2∧o=y) | 1 |
| ∃y(Syt1∧f=y) | 0 |
| ∃y(Syt2∧f=y) | 1 |
| ∃y(Syt1∧l=y) | 0 |
| ∃y(Syt2∧l=y) | 0 |
| ◊(∃y(Syt1∧o=y)) | 1 |
| ◊(∃y(Syt2∧o=y)) | 1 |
| ◊(∃y(Syt1∧f=y)) | ? |
| ◊(∃y(Syt2∧f=y)) | 1 |
| ◊(∃y(Syt1∧l=y)) | ? |
| ◊(∃y(Syt2∧l=y)) | ? |
| Cot1⇒◊(∃y(Syt1∧o=y)) | 1 |
| Cot2⇒◊(∃y(Syt2∧o=y)) | 1 |
| Cft1⇒◊(∃y(Syt1∧f=y)) | ? |
| Cft2⇒◊(∃y(Syt2∧f=y)) | 1 |
| Clt1⇒◊(∃y(Syt1∧l=y)) | ? |
| Clt2⇒◊(∃y(Syt2∧l=y)) | ? |
| Ho⇒(Cot1⇒◊(∃y(Syt1∧o=y))) | 1 |
| Ho⇒(Cot2⇒◊(∃y(Syt2∧o=y))) | 1 |
| Hf⇒(Cft1⇒◊(∃y(Syt1∧f=y))) | ? |
| Hf⇒(Cft2⇒◊(∃y(Syt2∧f=y))) | 1 |
| Hl⇒(Clt1⇒◊(∃y(Syt1∧l=y))) | ? |
| Hl⇒(Clt2⇒◊(∃y(Syt2∧l=y))) | ? |
| ∀tα(Ho⇒(Cotα⇒◊(∃y(Sytα∧o=y)))) | 1 |
| ∀tα(Hf⇒(Cftα⇒◊(∃y(Sytα∧f=y)))) | ? |
| ∀tα(Hl⇒(Cltα⇒◊(∃y(Sytα∧l=y)))) | ? |
| ∀x∀tα(Hx⇒(Cxtα⇒◊(∃y(Sytα∧x=y)))) | 1 |
| □∀x∀tα(Hx⇒(Cxtα⇒◊(∃y(Sytα∧x=y)))) | 1 |
De berekeningen in deze tweede waarheidstabel tonen dat formule 2 valide is.
Conclusie
In deze contemplatie gingen we erop uit om de kapitalistische slogan logisch te refuteren. Hiervoor moest deze slogan eerst verkend worden. Dit werd gedaan in de eerste paragraaf waar de slogan naar voren werd gebracht als 'in kapitalisme heeft iedereen de kans om succesvol te zijn'. Na een zeer korte introductie in modale eerste-orde-predicaten-logica in de tweede paragraaf werd de kapitalistische slogan logisch geformuleerd in de derde paragraaf. Twee formules werden gevonden. De eerste formule, '□∀x∀tα(Hx⇒(Cxtα⇒◊Sxtα))', beweert dat het noodzakelijk is voor elk wezen op elk tijdstip dat als dit wezen mens is het zo is dat als hij leeft in een kapitalistisch systeem op een bepaald tijdstip het mogelijk is dat hij succesvol is op dat tijdstip. Deze formule impliceert dat als één mens in een kapitalistisch systeem de mogelijkheid heeft op succes dat dan al zulke mensen die mogelijkheid moeten hebben op dezelfde tijd. De tweede formule, '□∀x∀tα(Hx⇒(Cxtα⇒◊(∃y(Sytα∧x=y))))', beweert dat het noodzakelijk is voor elk wezen op elk tijdstip dat als dit wezen mens is dat het zo is dat als hij in een kapitalistische samenleving leeft op een bepaald tijdstip het mogelijk is dat er een wezen is dat succesvol is op dat tijdstip en dat dat wezen die mens is die geplaatst is in de kapitalistische samenleving. Dat twee logische formules gegeven konden worden voor de kapitalistische slogan betekende dat deze slogan ambigu was. Deze ambiguïteit werd verkend in de vierde paragraaf. De kapitalistische slogan werd geclassificeerd als behorende tot het tweede type ambiguïteit. De logische betekenis van formule 1 is meer onverborgen dan die van formule 2. Aldus werden in de vijfde paragraaf de waarheidswaarden van beide formules berekend. De uitkomst was dat de waarheidswaarde van formule 1 niet bepaald kan worden op basis van de gebruikte data terwijl formule 2 met die data bepaald kan worden waar te zijn.
Bovenstaande moet ons tot de conclusie brengen dat de kapitalistische slogan zijn valide boodschap verbergt onder een onverborgen boodschap waarvan de validiteit niet bepaald kan worden. Hiermee positioneert hij zichzelf in een dubieuze positie. Want voor zover de kapitalistische slogan de boodschap van formule 2 overbrengt is zijn gebruik legitiem. Echter in het overbrengen van de betekenis van formule 1 is de legitimiteit van zijn gebruik zeer twijfelachtig. In principe gebruikt de kapitalistische slogan zijn valide betekenis om zijn gebruik te legitimeren, maar tegelijkertijd brengt hij een zeer twijfelachtige betekenis over. In de kapitalistische slogan wordt waarheid gebruikt met als doel het overbrengen van hetgeen zeer goed onwaarheid kan zijn. Maar dit is ronduit bedrog. De kapitalistische slogan is absoluut van een bedriegende aard en moet daarom krachtig gerefuteerd worden. Moge dit de actie zijn van allen die de kapitalistische slogan contempleren langs logische lijnen.
Noten
- Oxford English Dictionary, Second Edition on CD-ROM (v. 4.0), Oxford University Press, 2009, capitalism.
- Ibidem, capitalist.
- John Ayto, Word Origins, The Hidden Histories of English Words from A to Z, A & C Black, London, 2005, p. 462.
- Milton Friedman and Rose Friedman, Free to Choose, A Personal Statement, Harcourt Brace Jovanovich, New York / London, 1980, p. 146. "Wherever the free market has been permitted to operate, wherever anything approaching equality of opportunity has existed, the ordinary man has been able to attain levels of living never dreamed of before."
- Roy T. Cook, A Dictionary of Philosophical Logic, Edinburgh University Press, Edinburgh, 2009, p. 174.
- Ibidem, p. 264.
- Ibidem, p. 226.
- Ibidem, p. 236-237.
- Ibidem, p. 176.
- Ibidem, p. 191.
-
1. □∀x∀tα(Hx⇒(Cxtα⇒◊Sxtα)) ass 2. □∀tα(Ha⇒(Catα⇒◊Satα)) E∀1 3. □∃y∀tα(Hy⇒(Cytα⇒◊Sytα)) I∃2 4. □∃y∀tα(Hy⇒(Cytα⇒◊Sytα)) 3 5. □∀x∀tα(Hx⇒(Cxtα⇒◊Sxtα)) 1 6. □∃y∀tα(Hy⇒(Cytα⇒◊Sytα)) ⇒ □∀x∀tα(Hx⇒(Cxtα⇒◊Sxtα)) I⇒4, 5 - Word Origins, p. 22.
- Oxford Latin Dictionary, Oxford University Press, London, 1968, p. 113.
- Ibidem.
- Francis Edward Jackson Valpy, The Etymology of Words of the Greek Language, In Alphabetical Order, With the Omission Generally of Plants and Sometimes of the More Uncommon Animals, Longman, Green, Longman and Roberts, London, 1860, p. 11.
- Ibidem.
- Oxford Latin Dictionary, p. 87.
- The Etymology of Words of the Greek Language, p. 3.
- Monier Williams, A Sanskrit-English Dictionary, Etymologically and Philologically Arranged, With Special Reference to Greek, Latin, Gothic, German, Anglo-Saxon, and Other Cognate Indo-European Languages, The Clarendon Press, Oxford, p. 115, āj.
- A Dictionary of Philosophical Logic, p. 11.
Bibliografie
- John Ayto, Word Origins, The Hidden Histories of English Words from A to Z, A & C Black, London, 2005.
- Roy T. Cook, A Dictionary of Philosophical Logic, Edinburgh University Press, Edinburgh, 2009.
- Milton Friedman and Rose Friedman, Free to Choose, A Personal Statement, Harcourt Brace Jovanovich, New York / London, 1980.
- Francis Edward Jackson Valpy, The Etymology of Words of the Greek Language, In Alphabetical Order, With the Omission Generally of Plants and Sometimes of the More Uncommon Animals, Longman, Green, Longman and Roberts, London, 1860.
- Monier Williams, A Sanskrit-English Dictionary, Etymologically and Philologically Arranged, With Special Reference to Greek, Latin, Gothic, German, Anglo-Saxon, and Other Cognate Indo-European Languages, The Clarendon Press, Oxford.
- Oxford English Dictionary, Second Edition on CD-ROM (v. 4.0), Oxford University Press, 2009.
- Oxford Latin Dictionary, Oxford University Press, London, 1968.