Arvindus

Contemplations

Trisport

  • Title: Contemplations, Trisport.
  • Author: Arvindus.
  • Publisher: Arvindus.
  • Copyright: Arvindus, 2020, all rights reserved.
  • Index: 202004252.
  • Edition: html, second edition.
  • Original: Contemplaties, Trisport, Index: 202004251.

Content

Introduction

The point is the most elementary geometrical given. It carries the archetype of simplicity. Hegelian the point can be considered as a given on itself [an sich]. The point is the thesis.1

The line can be considered as the relation between two points. Contemporary math sometimes, unjustly, turns this consideration around, by defining a point as the intersection of two lines. From such a definition it could be deduced that lines are more elementary than points, however this is not the case. The points are the elementary givens which make the existence of lines possible.2 Now a line as a relation between two points is dual. A line represents reciprocity and opposition, namely that between the two points within which it is placed. Hegelian the line can therewith be considered as for itself [für sich]. The line is the antithesis.

When a third point is added then is come to a triangle, which could just as well be named a 'triline' or a 'tripoint', like a line could be called a 'twopoint'. For in a triangle three points are related to each other. The relationality within a triangle is thus triplicate. Dynamism is the archetype of the triangle. Hegelian the triangle can be considered as an on and for itself [an und für sich] given. The triangle is the synthesis.

Unisport and Bisport

The sketched archetypes of the point and the line we find also in our contemporary sports. The archetypes of the point we find in the so called 'performance sports'. We may think then of for instance athletics and power sports, where the sporter is actually only occupied with himself and primarily with the achieving of sportive results, which then possibly thereafter and secondary are compared with the achievements of other sporters. This is actually what also takes place during racing sports, be it that there the sports achievements of the individual sporters is not reached and measured chronologically but immediately. Characteristic of such 'unisports' is the given that the individual sporters are not directly relating to each other. Would they do that they would get disqualified.

The archetypes of the line are found in the so called 'game sports'. In these sports two sporting parties are directly opposed to each other. These sporting parties can be individuals and teams, think for instance of tennis and soccer. Here a sporter is not just occupied with the reaching of his own sporting achievements, but also with the going against the sporting achievements of the opposite party. Where in unisports only a winner is chosen on basis of the best uni-achievement, without any of the other unisporters can be announced as loser, there do 'bisports' know both winners and losers. The oppositionality of bisports involves this. This oppositional relation between two sporters or sport teams is characteristic of bisport.

Trisport

So where we see in contemporary sports unisports and bisports represented, we see trisports actually fully lacking. This is on itself remarkable since sport likes to present itself as a dynamic cultural element, while exactly trisport can introduce such dynamics in sports. This contemplation aims to contribute to the dynamication of sports.

What can a trisport look like? It shall be clear that where in unisport actually only one party is involved, and with bisport two parties, in trisport three parties will be involved. All the rest follows this given. Where in bisport the playing field is divided into two parts there it shall in trisport be divided into three parts. As an example a field as in figure 1 can be visualized.

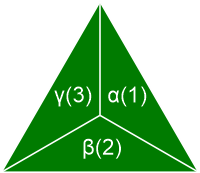
Trisport field

Figure 1.

We see a triangular field, divided into three parts (α, β, γ). The intention is that every part is the defensive part of one of the three parties (1, 2, 3). The field can also be designed as a round or hexagon model, as in figure 2. This will among other things be more attractive with an eye on the playing space and the to be arranged spectators.

Trisport round field

Figure 2.

From there the game can have its course according to two principles.

Principles

The two principles that were mentioned above have to do with the relation structures that underlie, or can underlie, triangularity, or trilinearity, or tripunctuality. In figure 2 below we see the three elementary points A, B and C with their relations visualized in lines AB (a), BC (b) and CA (c). Would we depict geometrically parties 1, 2 and 3 on the playing fields α, β and γ with their relations then we would get the same figure. With other words are the same principles underlying both sets of relations. So with a consideration on the nature of relations between points A, B and C we also directly get a view on the nature of relations between parties 1, 2 and 3.

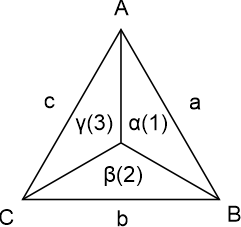
Trisport principles

Figure 3.

The above of course also goes for a round or hexagon field, as depicted below in figure 4.

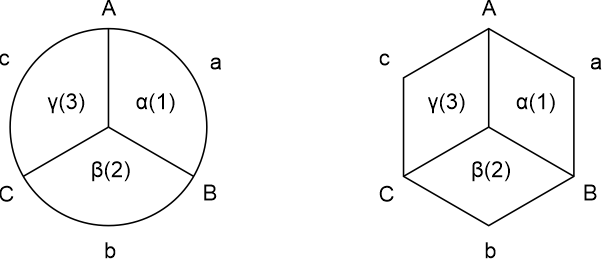
Trisport principles round field

Figure 4.

Uncoordinated Principle

Now trilinearity is in its base constructed from three oppositional relations, as they are to be found simply in bipunctuality or unilinearity, whereby every point knows two of such oppositional relations. However the whole is something different than the sum of its parts,3 and a trilinearity then is also something different than a set of three oppositional uniliniarities. Every point in a triangle, triline or tripoint has two reciprocal relations due to which a pure polarity, which is characterized by a simple opposition, is not the case. Every point may receive opposition of two other points, but at the same time the own opposition with regards to every other point is not the only opposition. We have to do with the relations A⇒B, B⇒A (A⇔B), A⇒C, C⇒A (A⇔C), B⇒C, C⇒B (B⇔C). This brings the oppositionality eventually to a stasis, proving the Hegelian correctness that the triangle as synthesis (the 'on and for itself') brings together the point as thesis (the 'on itself') and the line as antithesis (the 'for itself') in a trilateral way.

For trisport this principle of threefold reciprocity means that every of the three participating parties may receive opposition from, as also give it to, two other parties, but also that the giving of opposition to a certain party is not a simple case. With other words; where bisport is only characterized by competition, there trisport also brings cooperation in play. Party 1 and party 2 may cooperate against party 3, but party 3 also with party 1 against party 2, and party 2 also with party 3 against party 1. Cooperation is an important theme for the new age,4 and the enrichment of the world of sports with trisport may thus reflect this.

Coordinated Principle

Trisport can be worked out according to two principles and in the previous paragraph the uncoordinated principle was presented. 'Uncoordinated' means that there is no interference in the relations as they are contained in a natural way in the triangle. With trisport according to the coordinated principle this does happen. Thereby are certain relations which are contained within the triangle used, while others are put to rest. In the proposed coordinated principle under this paragraph the relations B⇒A, A⇒C and C⇒B are put to rest and only the relations A⇒B, B⇒C and C⇒A are maintained. For trisport this means that party 1 has to score with party 2, party 2 with party 3, and party 3 with party 1.

By putting the above mentioned relations to rest the element of cooperation may be removed from the triangle with its natural relations, however the element of reciprocity is therewith also removed. And the chaotic play of powers which takes place in uncoordinated trisport will be coordinated towards a circular set of relations.

Conclusion

Trisport shall bring much more dynamics in sports because it is built upon the principle of dynamics, which also underlies triangles. By integration of the element of cooperation, or at least by elimination of the element of reciprocal competition trisport shall be calibrated to the new age. The choice for uncoordinated or coordinated trisport is secondary, where choice for trisport is primary. In practise certain things have to be thought out further. In case of coordinated trisport for instance a change of party sequence has to take place (be it within one or within more games). Important however is that about the concept of trisport is thought and that is experimented with it. And to that this contemplation aims to be an incentive.

Bibliography
  • 'Academische filosofie, De subjectieve geest in zijn algemeenheid samengevat', Index: 200806261.
  • Aristotle, Metaphysica, in: The Works of Aristotle, Volume VIII, W. D. Ross (editor), Oxford University Press, London / et alibi, 1928.
  • Geert Crevits, Morya Wijsheid 4: Vertrouwen in jezelf, Mayil Publishing House, 2007.
  • Georg Wilhelm Friedrich Hegel, 'Wissenschaft der Logik', in: Philosophie von Platon bis Nietzsche, Directmedia, Berlin, 1998.